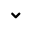2024 초은중 2학년 2학기 중간고사 분석
안녕하세요 무결 수학학원입니다!

24년 2학기 중간고사에 대한 분석과
앞으로 다가올 기말고사를 어떻게 준비해야하는지
설명하기 위해 왔습니다.

먼저 이번 시험의 난이도에 대해 알아보도록 하겠습니다!
이번 2024년 초은중학교 2학년 2학기 중간고사 문제는 학교 교과서 위주로 학습을 하고,
복습을 한 학생이라면 70점~80점대는 무난하게 받았겠으나 90점 이상의 고득점을 얻기는 힘들었을 것으로
보입니다. 90점 이상의 고득점을 얻기 위해서는 고난도 문제들을 꾸준히 학습하고, 복습하는 과정이 필수겠습니다. 이전의 시험에서는 고난도 문항들도 일반 시중 문제집에서 볼 수 있는 유형이 똑같이 출제가 되었다면,
이제는 동일한 유형이더라도 문제의 그림을 변형시키거나 구해야 하는 부분을 다르게 함으로써 새로운 문제로
변형시켜서 제출하는 경향이 높아지고 있습니다.
그러므로 앞으로의 시험을 대비할때는 문제의 답을 내는것도 중요하지만 문제를 분석할 수 있는 힘을 기를 수 있는 연습 또한 필요하겠습니다.
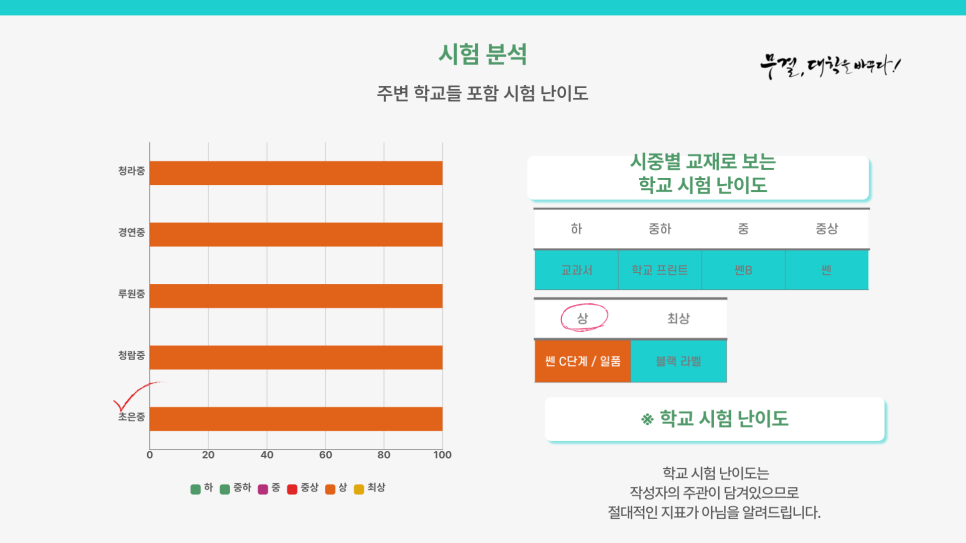
* 이번 초은중학교 2학년 2학기 중간고사 문제는 9번, 12번, 22번 이 3문제를 제외하고는 [교과서]와
[교과서 평가 문제집]에서 동일한 유형의 문제가 다수 출제가 되었다고 생각되어집니다.
* 9번, 12번, 22번 3문제에서 오답이 가장 많았을 것으로 생각되어집니다.
[9번 문항] : 접선의 개념, 그리고 내접원의 반지름과 삼각형의 둘레를 이용하여 삼각형의 넓이를 구하는 공식을
적용하면 문제를 해결 할수 있었습니다. 삼각형ABC의 넓이를 구하기 위해 피타고라스 정리를 활용해야 하는데
이부분을 떠올리지 못했다면 문제를 해결하기 어려웠을 것으로 보입니다.
[12번 문항] : 대부분 시중 문제집에는 사각형AFCE의 둘레의 길이나 한변의 길이를 구하는 문제가 많은데, 이 문제는 사각형AFCE의 대각선을 구하는 문제로 출제가 되었습니다. 이 문제는 주어진 길이와 삼각형 넓이를 이용하여
사각형AFCE의 넓이를 구하고, 피타고라스 정리를 활용하여 선분 AC의 길이를 구해 문제를 해결할 수 있습니다.
주어진 삼각형의 넓이로 변의 길이를 구하여 문제를 풀려고 접근하거나 마름모의 넓이를 대각선을 활용하여 구하는 공식을 잊었다면 문제를 해결하기 어려웠을 것으로 보입니다.
[22번 문항] : <쎈>이나 <일품>에서 학생들이 이 문제를 풀어본 경험은 많았을것으로 생각되어집니다.
그러나 이 문제에서 오답이 많았던 이유는 문제 출제 유형은 동일하지만 문제에 삽입된 그림을 부분만 제시함으로써 학생들로 하여금 새로운 문제처럼 인식하게 만들었기 때문이라고 생각되어집니다.
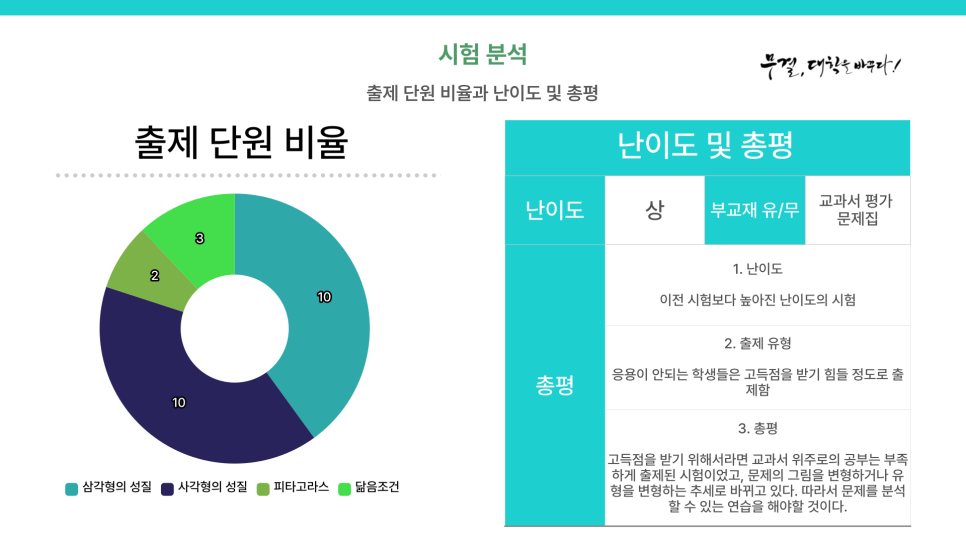
* 출제되는 5점 문항을 살펴보면 하나의 개념이 아닌 2-3개 이상의 개념을 활용하여 문제를 해결해야합니다.
기말대비시 고득점을 얻고자 한다면 심화학습이 필요하며,
변형문제 또한 해결할 수 있도록 탄탄한 학습이 필요하겠습니다.
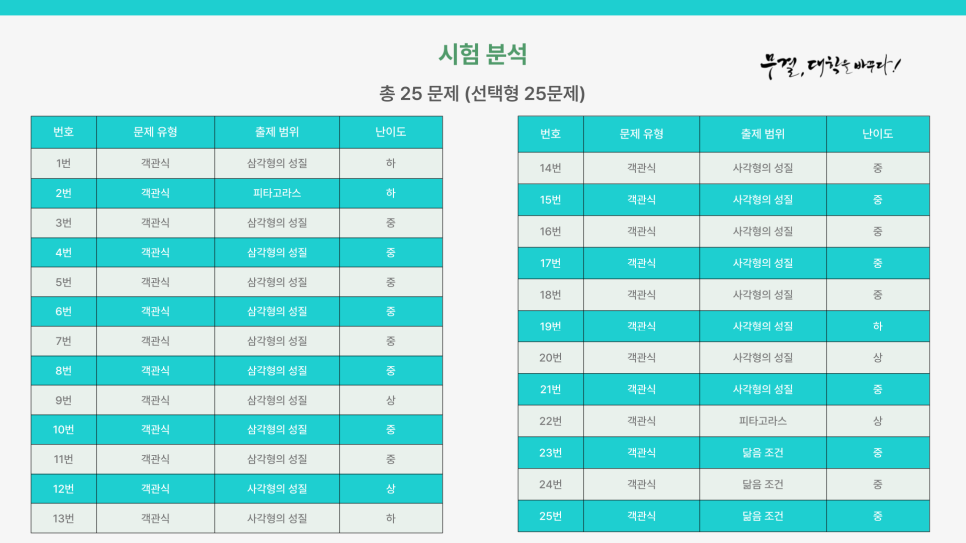
문제의 80%가 [도형의 성질] 단원에서 출제가 되었음을 알 수 있습니다. 나머지 20%가 [피타고라스의 정리],
[닮음 조건] 단원에서 출제가 되었고, [피타고라스의 정리] 단원에서 출제가 된 22번 문항이 이번 시험에서 가장
난이도가 높은 문제였습니다.
다음으로는 핵심 문항 및 킬러 문항 풀이입니다!
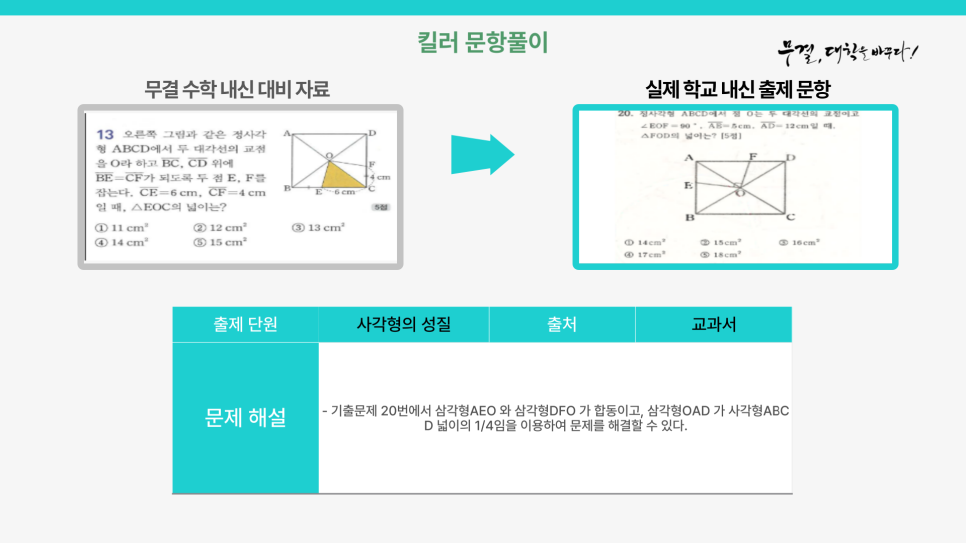
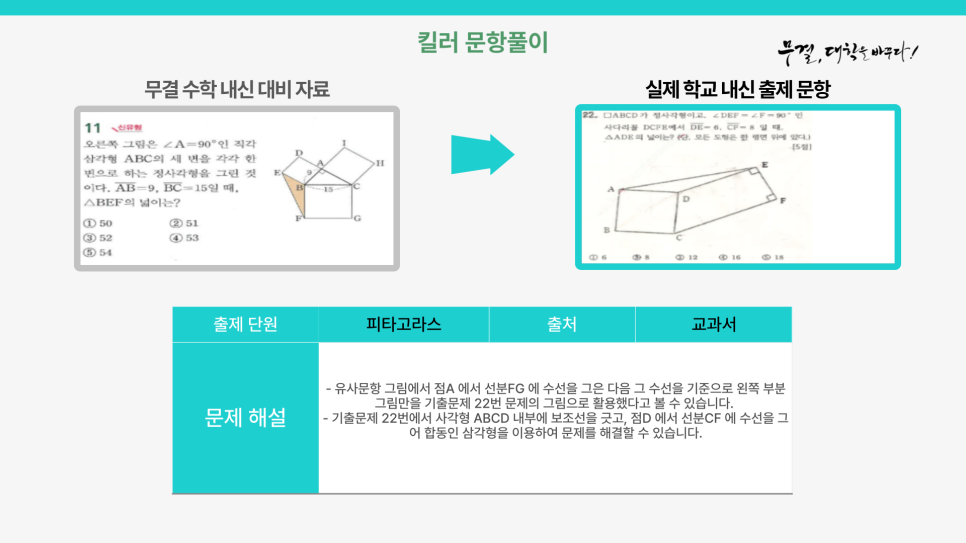
보시는 바와 같이 무결 수학 내신 대비 자료와 100%일치하는 문항이 실제 시험에 출제되었습니다!!

무결 수학만의 단계별,수준별 커리큘럼으로
완벽한 내신 대비!
이렇게 초은중2 중간고사 내신 분석을 해봤습니다!
다른 학교 시험 분석도
순차적으로 업로드 하도록 하겠습니다!
감사합니다!
무조건
결과로 증명합니다.
<찾아 오시는 길>